Euclides, el famoso matemático del siglo IV a.C., es conocido como el padre de la geometría. Sus teoremas han sido un pilar fundamental para el desarrollo de la matemática moderna. A continuación, exponemos diez ejemplos prácticos que ilustran estas reglas valiosas.
Ejemplo 1: Teorema de los Elementos
En su obra «Los Elementos», Euclides plantea el conocido postulado de las paralelas: «Por un punto exterior a una línea, solo se puede trazar una paralela». Este principio ha sido la base para el desarrollo de la geometría plana.
Ejemplo 2: Principio de superposición
Este teorema establece que si dos figuras planas coinciden al superponerse, estas son iguales en todas sus propiedades. Un ejemplo sencillo sería comparar dos hojas de papel de igual tamaño y forma.
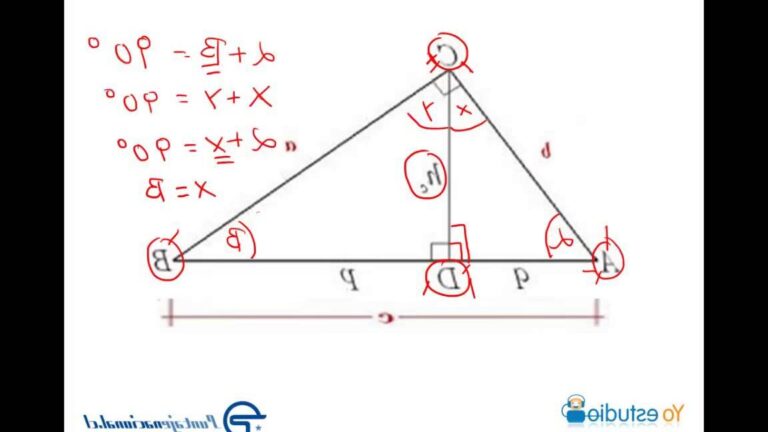
Ejemplo 3: Teorema del Ángulo Exterior
Según este teorema, cualquier ángulo exterior de un triángulo es igual a la suma de los dos ángulos interiores no adyacentes.
Ejemplo 4: Teorema de la suma de los ángulos de un triángulo
De acuerdo con Euclides, la suma de los ángulos internos de un triángulo siempre es igual a 180 grados.
Ejemplo 5: Propiedad de los círculos
Los radios de un mismo círculo siempre son iguales entre sí. Este es un principio fundamental en la construcción de círculos y esferas.
Ejemplo 6: Teorema del segmento medio en un triángulo
En un triángulo, el segmento que une los puntos medios de dos de sus lados es paralelo al tercer lado y mide la mitad que éste.
Ejemplo 7: Teorema de Pitágoras
Quizás uno de los más conocidos, determina que en un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.
Ejemplo 8: Teorema de la Bisectriz
La bisectriz de un ángulo de un triángulo divide el lado opuesto en dos segmentos que son proporcionales a los otros dos lados del triángulo.
Ejemplo 9: Teorema de Thales
Este teorema postula que cualquier diámetro de una circunferencia que subtenda un ángulo en la semicircunferencia opuesta, generará siempre un ángulo recto.
Ejemplo 10: La existencia del infinito
Aunque no sea un teorema en el sentido tradicional, Euclides fue uno de los primeros en reconocer la existencia del concepto de infinito en matemáticas.