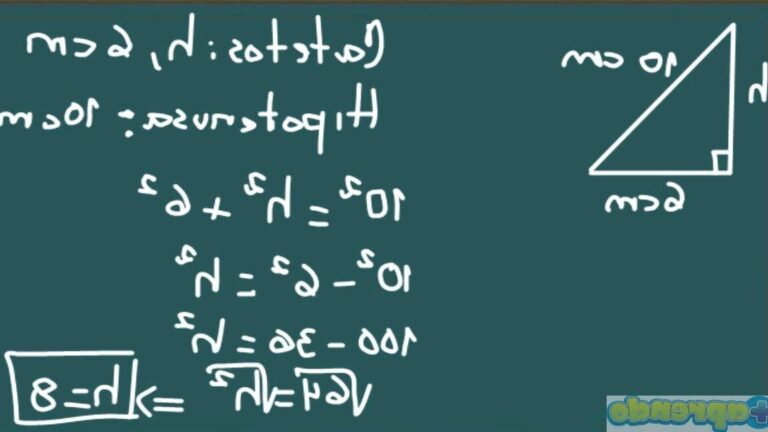10 Ejemplos de Teoremas de Pitágoras
El teorema de Pitágoras es uno de los pilares fundamentales de la geometría y las matemáticas en general. En esencia, este teorema establece que en un triángulo rectángulo, el cuadrado de la longitud de la hipotenusa (el lado más largo, opuesto al ángulo recto) es igual a la suma de los cuadrados de las longitudes de los otros dos lados. A continuación presentamos 10 ejemplos prácticos del teorema de Pitágoras que nos ayudarán a comprender mejor su aplicación y utilidad.
Ejemplo 1: Triángulo rectángulo con lados de 3 cm, 4 cm y 5 cm
Este es tal vez el ejemplo más sencillo y conocido de todos. Si tomamos un triángulo rectángulo con lados de 3 cm y 4 cm, aplicando el teorema de Pitágoras encontramos que el cuadrado de la hipotenusa es 25, lo cual indica que tiene 5 cm de longitud.
Ejemplo 2: Triángulo rectángulo con lados de 5 cm, 12 cm y 13 cm
En este segundo ejemplo, un triángulo rectángulo con lados de 5 cm y 12 cm tiene una hipotenusa cuyo cuadrado suma 169. Por lo tanto, su longitud es de 13 cm.
Ejemplo 3: Escalera apoyada en una pared
Imagine que tienes una escalera de 5 metros de longitud que está apoyada contra una pared. La base de la escalera está a 3 metros de la pared. ¿A qué altura alcanza la escalera en la pared? Aplicando el teorema de Pitágoras, obtenemos que alcanza a unos 4 metros de altura.
Ejemplo 4: Cálculo de la diagonal de un rectángulo
Si tienes un rectángulo de dimensiones 3×5, puedes calcular la longitud de la diagonal aplicando el teorema de Pitágoras. En este caso, la diagonal mide aproximadamente 5.83 unidades.
Ejemplo 5: Distancia entre dos puntos en un plano
Si deseas conocer la distancia entre dos puntos en un plano, puedes trazar un triángulo rectángulo utilizando los puntos como vértices y luego aplicar el teorema de Pitágoras para hallar la distancia.
Ejemplo 6: Área de un triángulo isósceles
Conociendo las longitudes de los tres lados de un triángulo isósceles, puedes aplicar el teorema de Pitágoras para calcular el área de ese triángulo.
Ejemplo 7: Diagonal de un cubo
La longitud de la diagonal de un cubo de lado a puede ser calculada aplicando el teorema de Pitágoras. En este caso, la longitud de la diagonal será a√3.
Ejemplo 8: Altura de un edificio
Si se encuentra a una cierta distancia de un edificio y se conoce el ángulo de inclinación de la vista hacia la cima de este, se puede usar el teorema de Pitágoras para calcular la altura del edificio.
Ejemplo 9: Longitud de la sombra de un objeto
Durante las horas del día, la sombra de un objeto se proyecta sobre el suelo formando un ángulo con el objeto. Conociendo la altura del objeto y el ángulo de inclinación de la luz, se puede usar el teorema de Pitágoras para calcular la longitud de la sombra.
Ejemplo 10: Distancia de la tierra a un satélite
Si se conoce la altitud de un satélite y el ángulo de elevación de la vista hacia este desde un punto en la tierra, se puede utilizar el teorema de Pitágoras para calcular la distancia total hasta el satélite.